Breath First Search

2022-03-09 389 words 2 minutes

Contents

Theory

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root(or some arbitrary node of a graph, sometimes referred to as a ‘search key’), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.

Implementation

Intuitively the breadth-first search prefers to visit the neighbors of earlier visited nodes before the neighbors of more recently visited ones. Let us reexamine the example we used in the depth-first search to see this change in action.

explanation

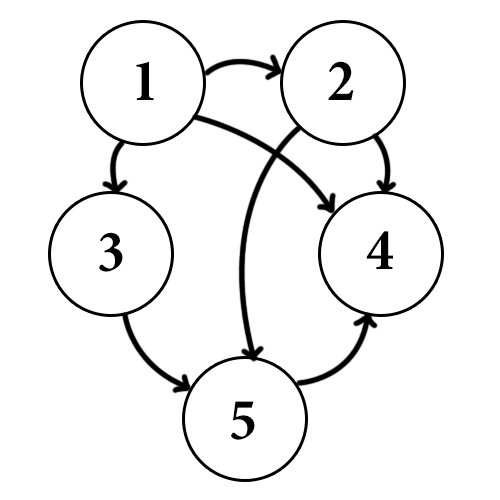
Starting again with vertex 1, we add 4, 3, and 2 (in that order) to our data structure, but now we prefer the first thing added to our data structure instead of the last.

That is, in the next step we visit vertex 4 instead of vertex 2. Since vertex 4 is adjacent to nobody, the recursion ends and we continue with vertex 3.

Now vertex 3 is adjacent to 5, so we add 5 to the data structure.

And then, we process vertex 2 before we process vertex 5.

Data structure for implementation

instead of using a stack we’ll use a queue. Again in the abstract, a queue is a data structure for which we’d like the following properties:

We can quickly add items to the queue.
We can quickly remove the least recently added item.

The operations on a queue are usually called enqueue (for additions) and dequeue (for removals).

Implement it based on dequeue

Note that a deque can also operate as a stack (it also has an append function with functions as the push operation). So in the following code for the breadth-first search, the only modification required to make it a depth-first search is to change the word “appendleft” to “append” (and to update the variable names from “queue” to “stack”).

And so the code for the breadth-first search algorithm is essentially identical:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


from collections import deque
 
def breadthFirst(startingNode, soughtValue):
   visitedNodes = set()
   queue = deque([startingNode])
 
   while len(queue) > 0:
      node = queue.pop()
      if node in visitedNodes:
         continue
 
      visitedNodes.add(node)
      if node.value == soughtValue:
         return True
 
      for n in node.adjacentNodes:
         if n not in visitedNodes:
            queue.appendleft(n)
   return False