Depth First Search

2022-03-09 536 words 3 minutes

Contents

Theory

Depth-first search (DFS) is an algorithm for traversing or searching graph or tree 🎄 data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux🧐 as a strategy for solving mazes.

Implementation

At the below, we will implement it in two ways, iterative and recursive.

Implement it in a recursive way

Depth-first search is inherently a recursion:

Start at a vertex.
Pick any unvisited vertex adjacent to the current vertex, and check to see if this is the goal.
If not, recursively apply the depth-first search to that vertex, ignoring any vertices that have already been visited.
Repeat until all adjacent vertices have been visited.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13



def depthFirst(node, soughtValue, visitedNodes):
   if node.value == soughtValue:
      return True
 
   visitedNodes.add(node)
   for adjNode in node.adjacentNodes:
      if adjNode not in visitedNodes:
         if depthFirst(adjNode, soughtValue, visitedNodes):
            return True
 
   return False

Implement it in a iterative way

At each vertex, push the adjacent vertices onto a stack in the reverse order that you iterate through the list. To choose which vertex to process next, simple pop whatever is on top of the stack, and process it (taking the stack with you as you go). Once again, we have to worry about which vertices have already been visited, and that part of the algorithm remains unchanged.

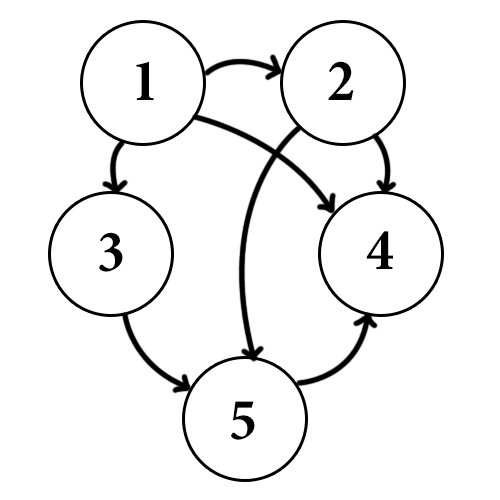
For example, say we have the following graph:

explanation

Starting at vertex 1, which is adjacent to vertices 2, 3 and 4, we push 4 onto the stack, then 3, then 2. Next, we pop vertex 2 and iteratively process 2. Since 2 is connected to 4 and also 5, we push 5 and then 4 onto the stack. Note that 4 is in the stack twice (this is okay, since we are maintaining a set of visited vertices). Now the important part is that since we added vertex 5 and 4 after adding vertex 3, those will be processed before vertex 3. That is, the neighbors of more recently visited vertices (vertex 2) have a preference in being processed over the remaining neighbors of earlier ones (vertex 1). This is precisely the idea of recursion: we don’t finish the recursive call until all of the neighbors are processed, and that in turn requires the processing of all of the neighbors’ neighbors, and so on.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19



def depthFirst(startingNode, soughtValue):
   visitedNodes = set()
   stack = [startingNode]
 
   while len(stack) > 0:
      node = stack.pop()
      if node in visitedNodes:
         continue
 
      visitedNodes.add(node)
      if node.value == soughtValue:
         return True
 
      for n in node.adjacentNodes:
         if n not in visitedNodes:
            stack.append(n)
   return False

advanteges

this version of the algorithm removes the issue with the return values. It is quite easy to tell when we’ve found the required node or determined it is not in the graph. if the loop terminates naturally (that is, without hitting a return statement), then the sought value doesn’t exist.