Divide and Conquer Algorithms

2022-03-15 567 words 3 minutes

Contents

Theory

In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.

Merge Sort

In computer science, merge sort (also commonly spelled as mergesort) is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort (stable sort algorithms sort equal elements in the same order that they appear in the input), which means that the order of equal elements is the same in the input and output. Merge sort is a divide and conquer algorithm.

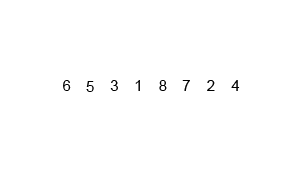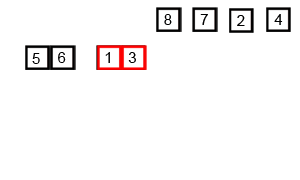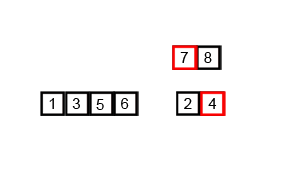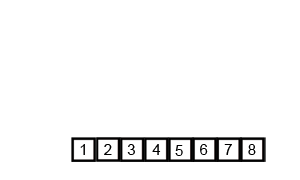
Example

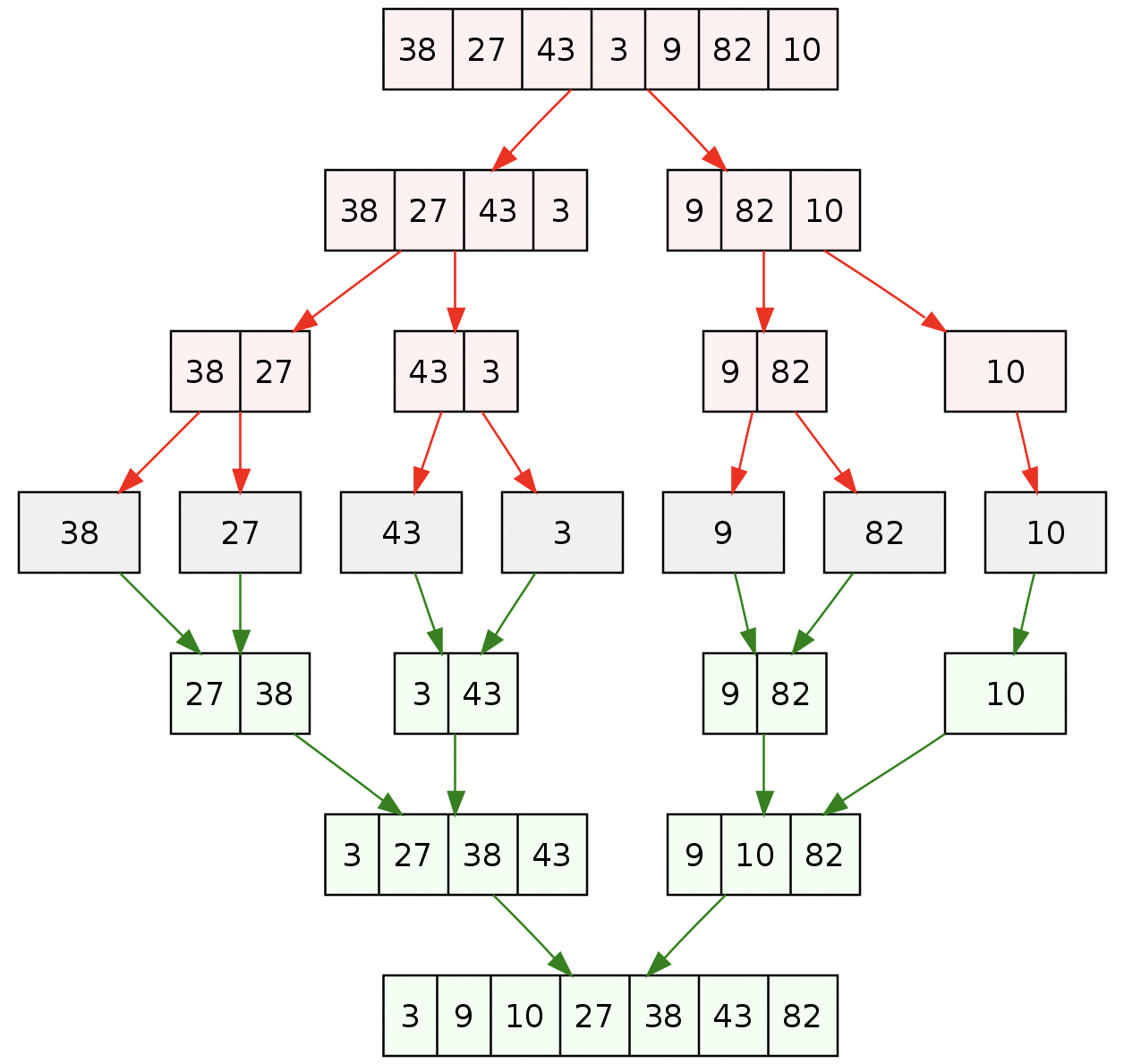
Conceptually, a merge sort works as follows:

Divide the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).
Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.

Master Theorem

The master method is a formula for solving recurrence relations of the form:

description

T(n) = aT(n/b) + f(n), where,

n = size of input
a = number of subproblems in the recursion
n/b = size of each subproblem. All subproblems are assumed to have the same size.
f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions.

Here, a ≥ 1 and b > 1 are constants, and f(n) is an asymptotically positive function.

The master theorem is used in calculating the time complexity of recurrence relations (divide and conquer algorithms) in a simple and quick way.

If a ≥ 1 and b > 1 are constants and f(n) is an asymptotically positive function, then the time complexity of a recursive relation is given by:

description

T(n) = aT(n/b) + f(n)

where, T(n) has the following asymptotic bounds:

If f(n) = O(n^logb(a-ϵ)), then T(n) = Θ(n^logb(a)).
If f(n) = Θ(n^logb(a)), then T(n) = Θ(n^logb(a) * log n).
If f(n) = Ω(n^logb(a+ϵ)), then T(n) = Θ(f(n)).

ϵ > 0 is a constant.

Each of the above conditions can be interpreted as:

If the cost of solving the sub-problems at each level increases by a certain factor, the value of f(n) will become polynomially smaller than n^logb(a). Thus, the time complexity is oppressed by the cost of the last level ie. n^logb(a)
If the cost of solving the sub-problem at each level is nearly equal, then the value of f(n) will be n^logb(a). Thus, the time complexity will be f(n) times the total number of levels ie. n^logb(a) * log(n)
If the cost of solving the subproblems at each level decreases by a certain factor, the value of f(n) will become polynomially larger than n^logb(a). Thus, the time complexity is oppressed by the cost of f(n).

solved example problem

T(n) = 3T(n/2) + n^2 Here,

a = 3

n/b = n/2

f(n) = n^2

K = 2

logb(a) = log2(3) ≈ 1.58 < 2

ie. f(n) < n^logb(a+ϵ) , where, ϵ is a constant.

Case 3 implies here.

Thus, T(n) = f(n) = Θ(n^2)

The master theorem cannot be used if:

T(n) is not monotone. eg. T(n) = sin n
f(n) is not a polynomial. eg. f(n) = 2n
a is not a constant. eg. a = 2n
a < 1