Graphs

Theory

G(Graph) = E(Edges) + V(Vertices)

Graph can be:

• Directed or undirected(also called bidirected)
• Cyclic or acyclic
• Connected or disconnected

Representation

Adjacency Matrix: Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][].

• a slot adj[i][j] = 1 indicates that there is an edge between vertex i and vertex j.
• Adjacency matrix for undirected graph is always diagonally symmetric.
• Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.

Sparse graph are more common in real life, but if we use adjacency matrix for a sparse graph then most of the matrix cells remain unused which leads to the waste of memory. Thus we prefer adgacency list for sparse graph.

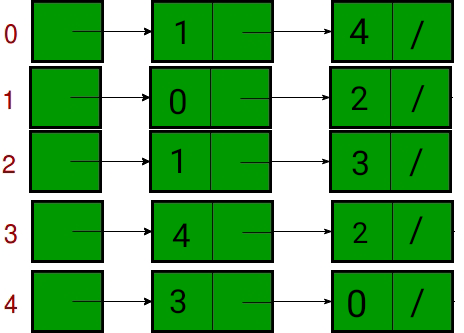
Adjacency List: An Adjacency list is an array consisting of the address of all the linked lists. The first node of the linked list represents the vertex and the remaining lists connected to this node represents the vertices to which this node is connected.

• This data structure can also be used to store additional data on the vertices. Additional data can be stored if edges are also stored as objects.
• The linked list can slightly be changed to even store the weight of the edge.
• it’s not necessary to be a linked list, other lists or arrays works as well.

When coding:

1
2
3
4
5
6
7
8

List<List<Integer>> graph

index    0 		  1 	  2 		3
	[[1,2,3,4], [0,3], [0,3,4], [0,1,2,4]]

for (Integer i : graph.get(0)) {
	// i is a neighbor of node 0
} 

Characteristics

• Adjacent node: A node ‘v’ is said to be adjacent node of node ‘u’ if and only if there exists an edge between ‘u’ and ‘v’.
• Degree of a node: In an undirected graph the number of nodes incident on a node is the degree of the node. In case of directed graph, Indegree of the node is the number of arriving edges to a node. Outdegree of the node is the number of departing edges to a node.
• Path: A path of length ‘n’ from node ‘u’ to node ‘v’ is defined as sequence of n+1 nodes. $$P(u,v)=(v0,v1,v2,v3…….vn)$$ A path is simple if all the nodes are distinct, exception is source and destination are same.
• Isolated node: A node with degree 0 is known as isolated node.Isolated node can be found by Breadth first search(BFS).

Types

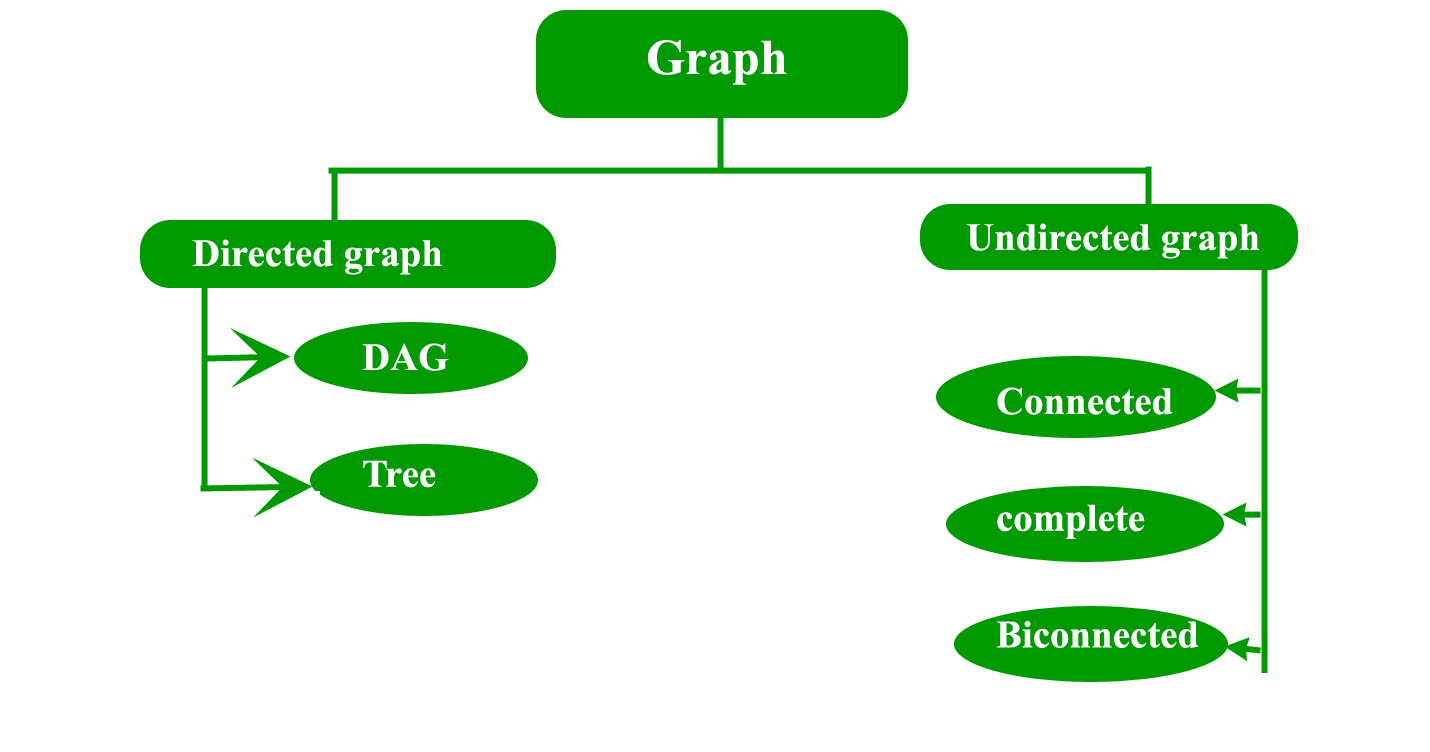
Directed graph: A graph in which the direction of the edge is defined to a particular node is a directed graph.

• Directed Acyclic graph: It is a directed graph with no cycle.For a vertex ‘v’ in DAG there is no directed edge starting and ending with vertex ‘v’. (Application :Critical game analysis,expression tree evaluation,game evaluation.)
• Tree: A tree is just a restricted form of graph. That is, it is a DAG with a restriction that a child can have only one parent.

Undirected graph: A graph in which the direction of the edge is not defined. So if an edge exists between node ‘u’ and ‘v’,then there is a path from node ‘u’ to ‘v’ and vice versa.

• Connected graph: A graph is connected when there is a path between every pair of vertices. In a connected graph there is no unreachable node.
• Complete graph: A graph in which each pair of graph vertices is connected by an edge. In other words, every node ‘u’ is adjacent to every other node ‘v’ in graph ‘G’. A complete graph would have $n(n-1)/2$ edges.
• Biconnected graph: A connected graph which cannot be broken down into any further pieces by deletion of any vertex. It is a graph with no articulation point 🧐.

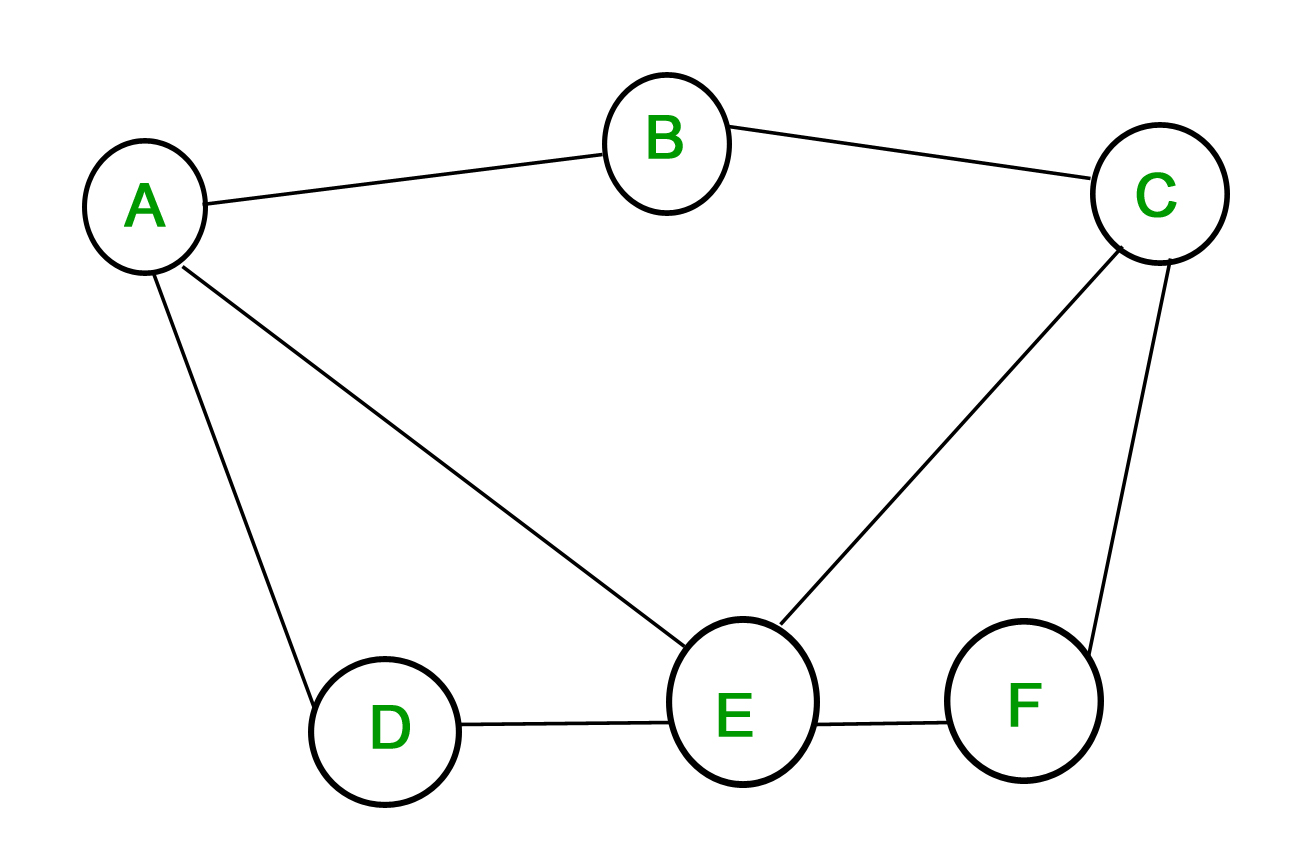
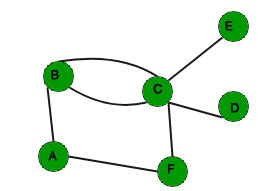
Simple graph: A graph in which each edge connects two different vertices and where no two edges connect the same pair of vertices is called a simple graph. For example, the below graph is a simple graph, since no vertex has a self-loop and no two vertices have more than one edge connecting them.

Multigraph: A graph in which multiple edges may connect the same pair of vertices is called a multigraph. The multiplicity of edge tells the number of edges between two vertices.

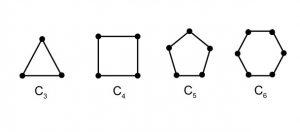
Some Special Simple Graphs

Cycles: Cycles are simple graphs with vertices n $\geq$ 3 and edges {1,2}, {2,3},…, {n-1, n} and {n,1}. Cycle with n vertices is denoted as $C_{n}$. Total number of edges are n with n vertices in cycle graph.

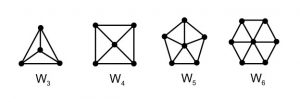
Wheels: A wheel is just like a cycle, with one additional vertex which is connected to every other vertex. Wheels of n vertices with 1 addition vertex are denoted by $W_{n}$. Total number of edges are 2*(n-1) with n vertices in wheel graph.

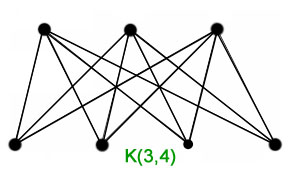
Bipartite Graphs: A simple graph G is said to be bipartite if its vertex set V can be divided into two disjoint sets such that every edge in G has its initial vertex in the first set and the terminal vertex in the second set.

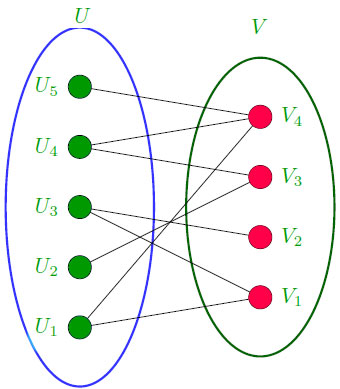
A bipartite graph with m and n vertices in its two disjoint subsets is said to be complete if there is an edge from every vertex in the first set to every vertex in the second set, for a total of m*n edges. A complete bipartite graph with m vertices in the first set and n vertices in the second set is denoted as $K_{m,n}$ .